じゃんけんの勝ち方を学習させるデモ
タイトルの通りAIにじゃんけんの勝ち方を学習させるデモを紹介します。
巷ではAIがプロ棋士に囲碁で勝ったという話題をよく目にしますが、 このページでは囲碁よりもずっと単純なじゃんけんについて、その勝ち方をAIに学習させる方法について説明します。
ここでいうAIというのは一体何なのか、AIにゲームの勝ち方を学習させるとはどういうことなのか、実際に何をしているのか。
一つひとつ説明します。
AIとは
物々しいタイトルをつけてはいますが、ここで厳密にAIの定義について語ることはしません。もしかしたらどこかの誰かがAIの厳密な 定義を定めているのかもしれませんが、ここでは機械学習の仕組みをある程度学んだ私の個人的な印象、所感を書きます。
「人工知能とかAIとか言ってるけど、ソフトウェア・ITシステムによる単なる自動化技術にAIという最もらしいラベルをつけてブランディングしてるだけじゃないの?」 と思ったことはありませんか?
これだけAIや機械学習が話題を集めている昨今、「AIを活用した〜システム」と書くだけで簡単に注目度を上げられてしまうため、 実際にはAIを活用していない似非AIシステムがマーケットに氾濫することは想像に難くありません。
とはいえ本当にAIのコンセプトが取り入れられているか素人が判断するのはなかなか難しいと思います。 私は「コアロジックをプログラムが持っているのかデータが持っているのか」が単なる自動化システムとAIを区別する最も重要なポイントだと考えています。
既存のITによる自動化技術では人が人力でロジックを組み立てます。例えば「ある条件を満たした時、ある値を返す」、 「こういう入力が入ってきたとき、こういう応答を返す」など、プログラマなどの「人」がどのような処理をすべきか ルールベースでソースコードに処理の手順や判定内容をハードコーディングしていきます。 このような似非AIは、あくまで設計者が「どのような組み合わせのデータが入力されてくるか」を事前にある程度想定しており、 想定されたデータをif then elseなどの制御構造を用いて条件分岐させながら出力するデータを作り上げていくという特徴があります。
それに対し、AIが用いる機械学習的な処理では、入力から出力を生成するのにプログラマが介在する条件分岐ロジックが存在しません。
(このあたりは専門家から物言いがつきそうですが、あくまで既存のITシステムとの違いを議論する文脈での話なので、厳密性についてははご容赦ください。)
これは「あるデータが入力された時、このデータを出力する」という処理をつくりたいと思った時、それをあらかじめプログラミングしないという意味です。
プログラミングするのではなく、こういう入力に対してはこういう出力をする、といった入力と出力の組み合わせのデータを大量に用意し、これを
学習させます。つまりAIがどのような振る舞いをするかは学習させるデータに依存し、AIのソースコードに処理方法はコーディングしません。
このページではAIにじゃんけんの勝ち方を学習させることがメインテーマですが、
AI側のロジックを一切変えず学習させるデータを変えることで「AIにじゃんけんの負け方」を学習させることも可能です。
ここで注意すべき点は、AIは学習データがなければ何もできない(精度が非常に低い)ということです。
AIがどのような学習データを利用しているか確認することは、似非AIと本物のAIを見分けるために非常に重要です。
例えば「あなたの会社に最適な人材をAIが自動で見つけます!」などという宣伝文句をみたら、気にすべきはAIの仕組みではありません。
使っているデータの種類とその量です。(理解の難しいAIの仕組みを確認しようとするより、データについて確認するほうがより有意義です。)
さらに踏み込めば、上のようなケースではデータの信頼性を(とりあえず)疑うことが非常に重要です。
100人程度のアンケートサンプルをAIに学習させたところで1億人にフィットするような汎用的な学習成果が果たして得られるか、
100人のアンケートから回答傾向を「外挿」し、100万人分のデータを同じ傾向に基づいて数だけ大量に自動生成していないか、などデータの由来を
考えることが非常に重要です。データの信頼性についてはAIや機械学習について深い知識がなくても簡単に質問できるので、気になるAIシステムがあれば
利用しているデータについて問い合わせると面白いと思います。
少し本題からそれてしまいました。あらためて本ページの目標を再確認しましょう。
目標
AIにじゃんけんの勝ち方を学習させる、とだけ書くと何やらとんでもなく複雑でものすごいことをしようとしているように見えますが、 実際にやることは非常に単純です。
ただ単に、相手がグーを出したらパー、チョキを出したらグー、パーを出したらチョキを出すことをプログラムに学習させるだけです。
通常のじゃんけんは手を同時に出しますが、ここでは後出しじゃんけん、つまり相手が手を出したのを見てこちらも出す手を決めるルールとします。
さて、これだけであれば機械学習やAIなどを使わなくとも
プログラミング言語を勉強したことのある人なら、すぐに下記のようなコードを思い浮かべるでしょう。
(下記のコードはRubyで書かれていますが、なんとなくやりたいことは解ると思います。)
def winning_hand(opponent_hand) return 'paa' if opponent_hand == 'guu' return 'guu' if opponent_hand == 'choki' return 'choki' if opponent_hand == 'paa' end
これは上で例に挙げたいわゆる人力でロジックを組むアプローチです。
たったこれだけのことをわざわざAIを持ちだして議論することに違和感を覚えるかもしれませんが、もう少し待ってください。
オセロもチェスも囲碁も、乱暴に書くと後出しじゃんけんを複雑にしただけのものです。じゃんけんの勝ち方をAIに学習させることを
理解できれば、その応用の先にオセロやチェス、囲碁の勝ち方をAIに学習させる方法が見えてくるはずです。
なお、チェス等のAIは強化学習という今回紹介するシンプルな機械学習の仕組みとは異なる仕組みを使っているので、このページを読んだだけで
チェスに勝てるAIを作れるようになるわけではありません。あしからず。
機械学習的アプローチ
ここからが本題です。AIにじゃんけんの勝ち方を学習させる具体的な方法について説明します。
まずはじゃんけんを機械学習で扱えるようモデル化します。
| 入力 | じゃんけんにおいて相手が出す手の確率。例えば[グー: 50%, チョキ: 30%, パー: 20%] |
| 出力 | 相手が出しそうな手に勝てる手。例えば相手がパーを出してくる確率が最も高いなら[グー: 0%, チョキ: 100%, パー: 0%] |
| NNタイプ | MLP(マルチレイヤーパーセプトロン) ※MLPについて詳細はこちらを参照。 |
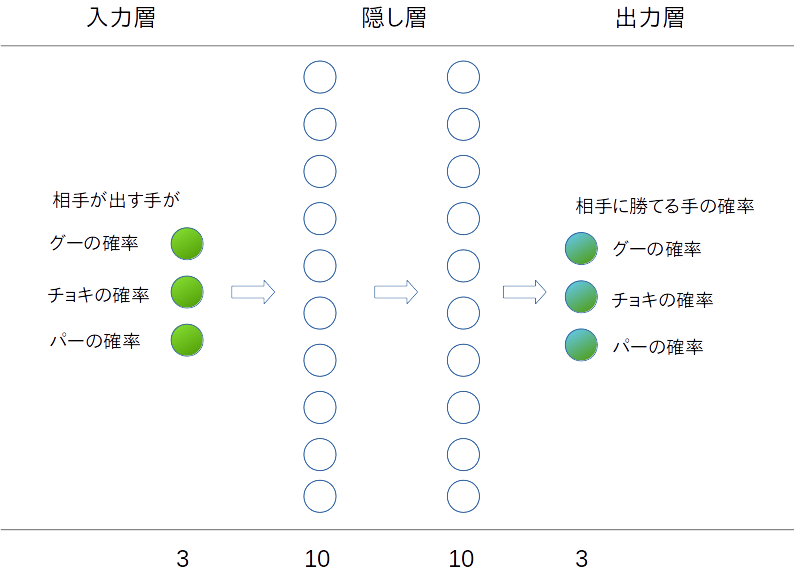
| レイヤー構成 | 3-10-10-3 (入力層、出力層のニューロンが3つずつ、中間の隠し層のニューロンが10個ずつである構成) |
上記のレイヤー構成を図示すると下記のようになります。
ニューラルネットワーク自体に「グーが出されたらパーを返す」ようなロジックをハードコーディングすることなく、 単に入出力層、隠し層のネットワーク構成が定義されているだけのプログラムをTensorFlowで作ります。
Python ソースコード
TensorFlowでAIにじゃんけんの勝ち方を学習させるソースコードです。要望があればソースコードを一つ一つ解説しますが、 まずはソースコードを自分で読んでみてください。できる限り易読化しようと努力はしました。
なお、MLPや入力がどのように計算されて出力を決めるのか、についてはTensorFlow Playgroundの仕組みでページを割いて説明しています。残念ですが、とても一言では説明できるものではないので機械学習本体の仕組みについては先のページで別途確認ください。
すでにTensorFlowを自分のローカルPCにインストール済みであれば、 下記のコードをコピー&ペーストして'janken.py'などのようなファイル名で保存し、そのままpythonで実行できます。
import os os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3' import numpy as np import tensorflow as tf import time import datetime as dt """ じゃんけん用学習データを生成するクラス。 本来であればプログラムでデータを自動生成するのではなく、 人が実際にじゃんけんをして得られる”手作り”データを用いる方が 「機械に人間の行動を学習させる」例としては良いのだが 今回は簡単なデモということでデータを自動生成させている。 """ class RockScissorsPaper: def __init__(self, number_of_data=1000): self.number_of_data = number_of_data # 相手が出すじゃんけんの手の確率 # 戻値:[グーを出す確率, チョキを出す確率, パーを出す確率] def opponent_hand(self): rand_rock = np.random.rand() rand_scissors = np.random.rand() rand_paper = np.random.rand() total = rand_rock + rand_scissors + rand_paper return [rand_rock/total, rand_scissors/total, rand_paper/total] # グーが来る確率が一番高かったらパー、 # チョキが来る確率が一番高かったらグー、 # パーが来る確率が一番高かったらチョキ # を返す。 # 引数:[グーが来る確率, チョキが来る確率, パーが来る確率] # 戻値:[グーを返すか否か(0or1), チョキを返すか否か(0or1), パーを返すか否か(0or1)] # # 例: # 引数が[0.6, 0.3, 0.1]の時、グーが来る確率が60%で最も高いため、 # グーに勝てるパーを出すため戻値は[0, 0, 1]となる。 def winning_hand(self, rock, scissors, paper) -> [float, float, float]: mx = max([rock, scissors, paper]) if rock == mx: return [0, 0, 1] if scissors == mx: return [1, 0, 0] if paper == mx: return [0, 1, 0] # この手が来た時にあの手を返すと勝てる、を集めた学習用データ def get_supervised_data(self, n_data=None): if n_data is None: n_data = self.number_of_data # トレーニングデータ生成 supervised_data_input = [] supervised_data_output = [] for i in range(n_data): rock_prob, scissors_prob, paper_prob = self.opponent_hand() input_probs = [rock_prob, scissors_prob, paper_prob] supervised_data_input.append(input_probs) supervised_data_output.append(self.winning_hand(*input_probs)) return {'input': supervised_data_input, 'output': supervised_data_output} """ ここからTensorFlowの機械学習用の処理 処理は下記の流れで実行 (1) 入力層の作成 (2) 隠し層、出力層の作成 (3) 誤差の定義 (4) 学習用TensorFlow Operationの作成 (5) 学習実行 (6) 学習結果検証 """ FLAGS = tf.app.flags.FLAGS tf.app.flags.DEFINE_string('summary-dir', '/tmp/tensorflow/summary', "TensorBoard用のログを出力するディレクトリのパス") tf.app.flags.DEFINE_integer('max-epoch', 100, "最大学習エポック数") tf.app.flags.DEFINE_integer('batch-size', 10, "1回のトレーニングステップに用いるデータのバッチサイズ") tf.app.flags.DEFINE_float('learning-rate', 0.07, "学習率") tf.app.flags.DEFINE_integer('test-data', 10, "テスト用データの数") tf.app.flags.DEFINE_integer('training-data', 1000, "学習用データの数") tf.app.flags.DEFINE_boolean('skip-training', False, "学習をスキップしてテストだけする場合は指定") def train_and_test(training_data, test_data): if len(training_data['input']) != len(training_data['output']): print("トレーニングデータの入力と出力のデータの数が一致しません") return if len(test_data['input']) != len(test_data['output']): print("テストデータの入力と出力のデータの数が一致しません") return # ニューラルネットワークの入力部分の作成 with tf.name_scope('Inputs'): input = tf.placeholder(tf.float32, shape=[None, 3], name='Input') with tf.name_scope('Outputs'): true_output = tf.placeholder(tf.float32, shape=[None, 3], name='Output') # ニューラルネットワークのレイヤーを作成する関数 def hidden_layer(x, layer_size, is_output=False): name = 'Hidden-Layer' if not is_output else 'Output-Layer' with tf.name_scope(name): # 重み w = tf.Variable(tf.random_normal([x._shape[1].value, layer_size]), name='Weight') # バイアス b = tf.Variable(tf.zeros([layer_size]), name='Bias') # 入力総和(バッチ単位) z = tf.matmul(x, w) + b a = tf.tanh(z) if not is_output else z return a # レイヤーを作成 # 3-10-10-3のDNN layer1 = hidden_layer(input, 10) layer2 = hidden_layer(layer1, 10) output = hidden_layer(layer2, 3, is_output=True) # 誤差の定義 with tf.name_scope("Loss"): # クロスエントロピー with tf.name_scope("Cross-Entropy"): error = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=true_output, logits=output)) # 真の出力と計算した出力がどれだけ一致するか with tf.name_scope("Accuracy"): accuracy = tf.reduce_mean(tf.cast(tf.equal(tf.arg_max(true_output, 1), tf.argmax(output, 1)), tf.float32)) * 100.0 with tf.name_scope("Prediction"): # 出力値を確率にノーマライズするOP(起こりうる事象の和を1にする) prediction = tf.nn.softmax(output) # 学習用OPの作成 with tf.name_scope("Train"): train_op = tf.train.GradientDescentOptimizer(FLAGS.learning_rate).minimize(error) # セッション生成、変数初期化 sess = tf.Session() sess.run(tf.global_variables_initializer()) # TensorBoard用サマリ writer = tf.summary.FileWriter(FLAGS.summary_dir + '/' + dt.datetime.now().strftime('%Y%m%d-%H%M%S'), sess.graph) tf.summary.scalar('CrossEntropy', error) tf.summary.scalar('Accuracy', accuracy) summary = tf.summary.merge_all() # 学習を実行する関数 def train(): print('----------------------------------------------学習開始----------------------------------------------') batch_size = FLAGS.batch_size loop_per_epoch = int(len(training_data['input']) / batch_size) max_epoch = FLAGS.max_epoch print_interval = max_epoch / 10 if max_epoch >= 10 else 1 step = 0 start_time = time.time() for e in range(max_epoch): for i in range(loop_per_epoch): batch_input = training_data['input'][i*batch_size:(i+1)*batch_size] batch_output = training_data['output'][i*batch_size:(i+1)*batch_size] _, loss, acc, report = sess.run([train_op, error, accuracy, summary], feed_dict={input: batch_input, true_output: batch_output}) step += batch_size writer.add_summary(report, step) writer.flush() if (e+1) % print_interval == 0: learning_speed = (e + 1.0) / (time.time() - start_time) print('エポック:{:3} クロスエントロピー:{:.6f} 正答率:{:6.2f}% 学習速度:{:5.2f}エポック/秒'.format(e+1, loss, acc, learning_speed)) print('----------------------------------------------学習終了----------------------------------------------') print('{}エポックの学習に要した時間: {:.2f}秒'.format(max_epoch, time.time() - start_time)) # 学習成果をテストする関数 def test(): print('----------------------------------------------検証開始----------------------------------------------') # ヘッダー print('{:5} {:20} {:20} {:20} {:2}'.format('', '相手の手', '勝てる手', 'AIの判断', '結果')) print('{} {:3} {:3} {:3} {:3} {:3} {:3} {:3} {:3} {:3}'.format('No. ', 'グー ', 'チョキ', 'パー ', 'グー ', 'チョキ', 'パー ', 'グー ', 'チョキ', 'パー ')) # 最も確率の高い手を強調表示するための関数 def highlight(rock, scissors, paper): mx = max(rock, scissors, paper) rock_prob_em = '[{:6.4f}]'.format(rock) if rock == mx else '{:^8.4f}'.format(rock) scissors_prob_em = '[{:6.4f}]'.format(scissors) if scissors == mx else '{:^8.4f}'.format(scissors) paper_prob_em = '[{:6.4f}]'.format(paper) if paper == mx else '{:^8.4f}'.format(paper) return [rock_prob_em, scissors_prob_em, paper_prob_em] # N回じゃんけんさせてみてAIが勝てる手を正しく判断できるか検証 win_count = 0 for k in range(len(test_data['input'])): input_probs = [test_data['input'][k]] output_probs = [test_data['output'][k]] # 検証用オペレーション実行 acc, predict = sess.run([accuracy, prediction], feed_dict={input: input_probs, true_output: output_probs}) best_bet_label = np.argmax(output_probs, 1) best_bet_logit = np.argmax(predict, 1) result = '外れ' if best_bet_label == best_bet_logit: win_count += 1 result = '一致' print('{:<5} {:8} {:8} {:8}'.format(*(tuple([k+1]+highlight(*input_probs[0])))), end='') print(' ', end='') print('{:8} {:8} {:8}'.format(*tuple(highlight(*output_probs[0]))), end='') print(' ', end='') print('{:8} {:8} {:8}'.format(*tuple(highlight(*predict[0]))), end='') print(' ', end='') print('{:2}'.format(result)) print('----------------------------------------------検証終了----------------------------------------------') print('AIの勝率: {}勝/{}敗 勝率{:4.3f}%'.format(win_count, FLAGS.test_data-win_count, (win_count/len(test_data['input']) * 100.0))) print('学習無しの素の状態でAIがじゃんけんに勝てるか確認') test() if not FLAGS.skip_training: train() print('学習後、AIのじゃんけんの勝率はいかに…!') test() def main(argv=None): # 学習用データ取得 janken = RockScissorsPaper() training_data = janken.get_supervised_data(FLAGS.training_data) test_data = janken.get_supervised_data(FLAGS.test_data) train_and_test(training_data, test_data) if __name__ == '__main__': tf.app.run()
上記のソースコードを自分の環境で実行するためにはマシンにTensorFlowをインストールが必要があります。
TensorFlowのインストール方法については本サイトでも他のページで解説していますが、CPUやGPUの最適化を考えずとりあえずデモが動けば良い程度で
あればpython3をマシンにインストールし管理者権限で`pip3 install --upgrade tensorflow`とコマンドを打てばWindowsでもLinuxでもTensorFlowを導入できます。
コード実行結果例
上記のコードを引数無しでそのまま実行すると、下記の処理が走ります。
- 相手のじゃんけんの手、およびその手に勝てる手の組み合わせのデータを1000セット生成
- 層構成が3-10-10-3のニューラルネットワーク(MLP)の計算グラフを作成
- 学習前の赤ん坊状態のAIにじゃんけんをさせてみて勝率を確認(当てずっぽうに手を出すので勝率は33%程度となる見込み。)
- 100エポック分上記の学習用データを使って機械学習開始。(1エポックの定義についてはこちらを参照)。
- 学習後、じゃんけんをさせAIの勝率を再度確認
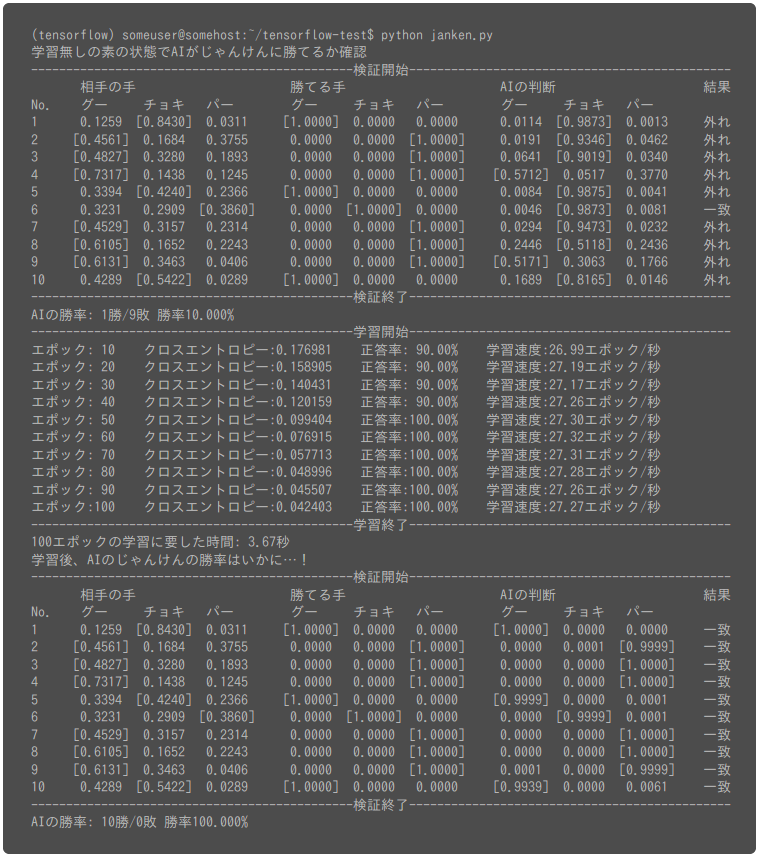
それでは試しにこのソースコードを実行して出力を確認してみましょう。
学習前は後出しじゃんけんでAIはどの手を出すべきか全くわかっていませんので当てずっぽうに手を出し、勝率は10%になっています。
そして学習後、たった10回の試行ではありますが、AIはどの手を出せば勝てるかきちんと学習していることがわかります。
テスト回数を増やしてみる
上記のpythonプログラムは引数でニューラルネットワークのパラメータをいくつか変えることができます。 例えば
のように--test-dataのオプションを使うと、この例ではAIのじゃんけんの勝率を100個のテストデータで検証することができます。
私の環境ではテストデータ100個のテストデータのテストを数回してみましたが、ほとんどのケースでAIが100勝0敗で勝率100%を達成していました。
まれに98勝2敗のようにAIが後出しじゃんけんに負けるケースも確認できました。
そういったケースでは下記のように、相手が出す手の確率が横並びになっており相手がどの手を出すかはっきりと断定しにくい状態が多く見られました。
相手が確実にグーを出してくるならパーを出せば良いと判断できますが、グーとパーを出す確率がほぼ同じであれば出す手に悩みますね。
こういったところは非常に人間的な判断に見えてしまいます。
AIに「じゃんけんの負け方を教える」
本ページ冒頭でデータを変えることでじゃんけんの負け方を学習させることが可能と書きました。 さて、それでは上記のソースコードをどう変えればAIにじゃんけんの負け方を教えることができるでしょうか。
答えは非常に単純です。学習用データを自動生成するクラスRockScissorsPaperの下記のメソッドをこっそり書き換えてやれば良いです。
# グーが来る確率が一番高かったらパー、 # チョキが来る確率が一番高かったらグー、 # パーが来る確率が一番高かったらチョキ # を返す。 # 引数:[グーが来る確率, チョキが来る確率, パーが来る確率] # 戻値:[グーを返すか否か(0or1), チョキを返すか否か(0or1), パーを返すか否か(0or1)] # # 例: # 引数が[0.6, 0.3, 0.1]の時、グーが来る確率が60%で最も高いため、 # グーに勝てるパーを出すため戻値は[0, 0, 1]となる。 def winning_hand(self, rock, scissors, paper) -> [float, float, float]: mx = max([rock, scissors, paper]) if rock == mx: return [0, 0, 1] if scissors == mx: return [1, 0, 0] if paper == mx: return [0, 1, 0]
このメソッドは相手が最も出しそうな手に勝てる手のデータを返します。
ここで、相手が最も出しそうな手に負ける手を返すようにメソッドを修正すれば
「相手が出した手に負ける手」の学習用データが大量生成され、AIは負けることをひたすら学習します。
このように、AI自身は自分が何を学習しているか全くわかっていません。 勝ち方を学習しているのか、負け方を学習しているのか、そもそもじゃんけんがテーマかすら認識していません。 あくまでデータの内容に意味付けをするのは我々人間です。AIは機械学習の数学に則って 真の出力と計算した出力との誤差が小さくなるようニューラルネットワークのパラメータの更新を繰り返すだけです。
ですのでAIを用いたシステムの品質を左右するのは本質的にはAI技術ではなくデータの品質です。(少なくとも私はそう考えています) 悪意を持って意図的に偏ったり誤った学習データをAIに学習させればその悪意が反映されたAIが出来上がります。
学習させるデータによってAIは善にも悪にもなりうる、そういったSFのような壮大な話が、 この単純なじゃんけんの学習を通じてその一端を理解できるというのは非常に感慨深いですね。
おまけ: Tensorboardの計算グラフ
ソースコードの中にTensorboard関連の処理を入れておきましたが、 このコードを実行して得られる計算グラフを参考までに紹介します。
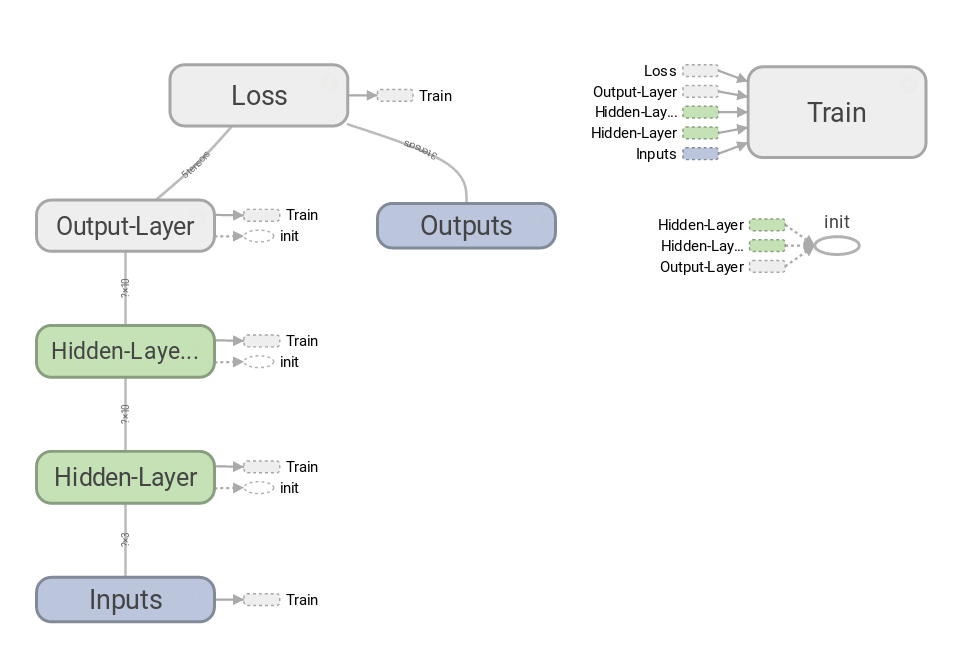
MLPのような単純なニューラルネットはこのように非常にシンプルなグラフになります。
CNN(畳み込みニューラルネット)やLSTMなどのRNN(再帰型ニューラルネット)ではより複雑なグラフになります。
以上です。ここまでお読みくださりありがとうございました。